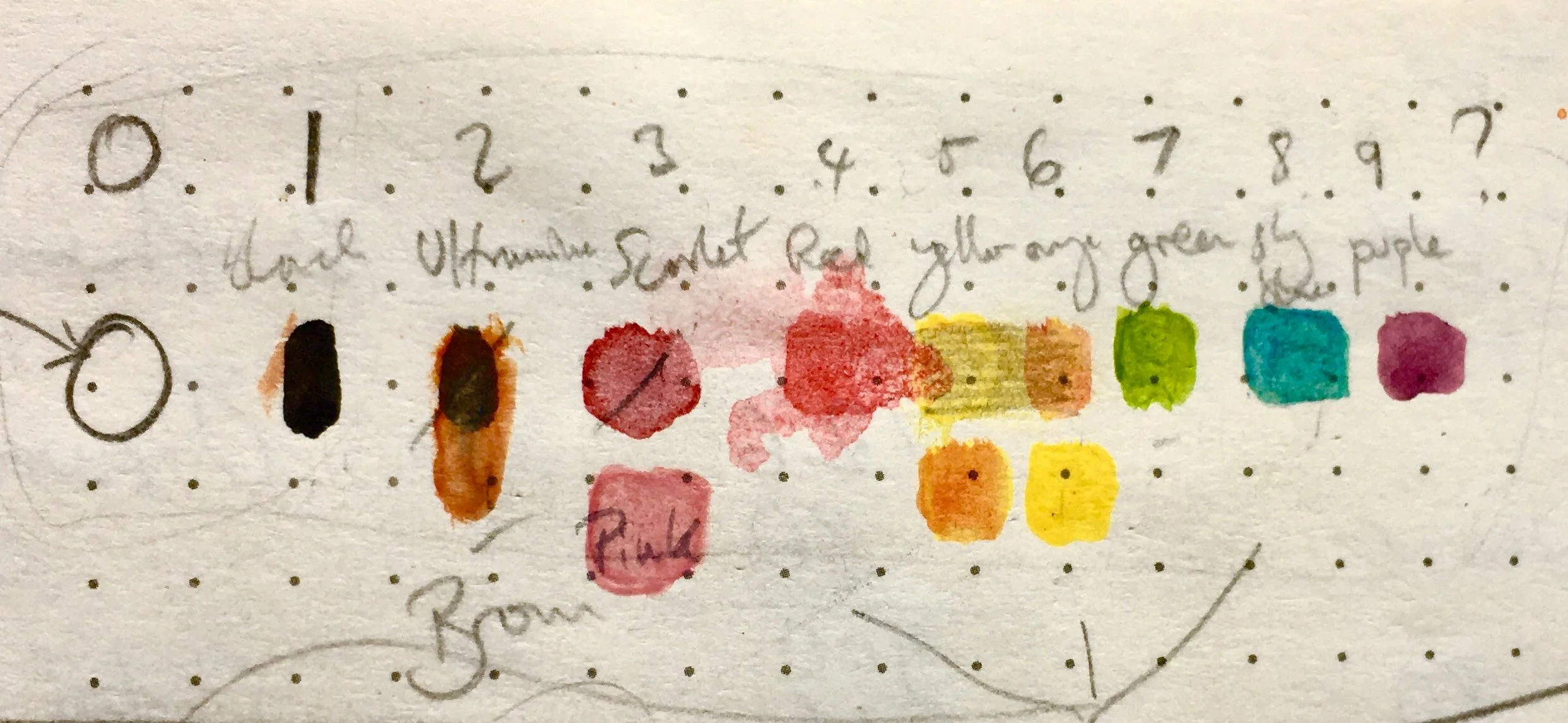PART ONE
SCRIBBLING IN MY SKETCHBOOK

There are things that this experience  - this “colourful language” -  has taught me, and helped me understand, that I’m not quite sure how to put into words. I’ve had many “Ah-ha!” moments of insight and clarity  -  like mountains appearing from behind clouds then disappearing again. But it’s not as simple as getting out your camera and taking a picture. You have to stop and write or draw it, on whatever’s available  -  which for me right means scribbling on an A1 sheet of tracing paper I’ve had folded up in my pocket and a big red sketchbook.

You have to catch these thoughts when they come. And that’s what I’ve been doing  -  or trying to do  -  over the past year or so with the thoughts that have come from painting maths. Thoughts and ideas of a new kind for me. I don’t really have a framework or reference for what kind of thoughts they are, or what area of study they belong to. But I’d like to know. And I’m hoping that by writing this, others might be able to guide me towards areas of study that could help me continue this journey  -  and understand these thoughts more deeply.

I’ve been making notes in my sketchbooks, on scraps of paper and on the backs of paintings made by children I’ve shared the method with. I’ve tried to collect them all and keep them arranged. But even when I’ve managed to write my thoughts down, I’ve found it difficult to express myself. I don’t quite know how to communicate what I’m thinking or realising. It’s sometimes been frustrating, as though I don’t have the words I need  -  as if I’ve come up against a barrier of language. Much like I felt with maths, I suppose.

But I want to write these things down, and to communicate whatever I can, in some way. Maybe some of that communication is best done through the maths itself - through the images and paintings I’ve created. Many times, I’ve felt deeply emotional while painting the maths: wordless feelings that rise up from I don’t know where. No story. No identifiable root. Hopefully, those images can say what I want to express. Because they themselves are expressions. Of something.

Before I get into it properly, I want to acknowledge that I’m not a trained specialist in educational studies, nor have I undertaken any formal study of teaching methods or pedagogy - a word I’d heard before but only recently learned the meaning of while reading The Glass Bead Game, a novel by the German author Hermann Hesse. It’s a story about knowledge, art, maths, music, and meditation, which ultimately emphasises how important education is: that no matter how impressive knowledge may be, its true value lies in how it’s passed on and shared.

As I say, I haven’t studied pedagogy, and I’m not writing this to come across as an “academic.” I am, however, a keen painter - and I love writing, whether that’s stories, poems, songs, music, or just thoughts in my journal. I thought it might be useful - if not for anyone else, then at least for myself - to write down the thoughts that have arisen from this experience, and from watching my art change so drastically before my eyes. Another reason I want to write this all down is because people have contacted me saying they want to reference my method in their master’s degrees and other studies. A few times, it’s even been mentioned that someone might one day carry out PhD research on it. That has inspired me to share my own feelings and findings too.

At the moment, I don’t have much data in the numerical, structured, graphable sense. But I do have feelings, examples, anecdotal and experiential data - and ideas. At times, these thoughts and ideas might be poetic or whimsical, but poetry and whimsical mystery have been key ingredients in what led me to create what I’ve created.

That’s what I do have. And as a “maker-of-things” I’ve always tried to make do with whatever I have to hand. I once made a giraffe from an old curtain and a tree branch, and a whale from a garden parasol. When I was about ten or eleven, I made a flying machine out of lollypop sticks, bottle tops, a plastic bag - and lots of glue. With the help of an elastic band it flapped its wings and very slowly moved across the dinner table... but it didn’t fly. Unfortunately, that was before camera phones, so the last I saw of it was as I crushed it into the bin under the kitchen sink. It didn’t work (i.e. fly), and it was just gathering dust. (It very much flew in my imagination.)

Basically, I love making things. And it’s surprising what you can make with bits and bobs lying around. That’s what this ‘essay’ is going to be made from: bits and bobs from my brain - the whimsical, poetic, light-hearted, and at times deeply sincere thoughts, ideas, hopes, and feelings from experiencing a year of maths in multicolour.

To give a bit of context, I am writing this as I am trekking up through the Solukhumbu region in Nepal, most famous for being home to Sagarmatha, or Mount Everest as it’s known in the West. I am not a trekker, I’m not even a hiker. A few months ago this was not at all something even remotely on my mind, but a series of conversations, chance meetings and enthusiastic maths lessons has led me here. I’ve been a little nervous about doing this, but as soon as I started a few days ago I feel a great buzz of energy. The purpose behind this trek is to teach multicolour maths in the schools I pass along the way to Everest Base Camp, where I will wave a flag covered with colourful maths painted by the children I teach. After having taught in the schools already, in Jubing and Kharikhola, it is turning into one of the most beautiful and unexpected adventures – to be teaching maths up the mountain. So that is where I find myself at this moment, making a journey, step by step up a very long hill, through clouds, past rivers, alongside incredibly strong Sherpas carrying loads of unbelievable weight, and at times behind donkeys. Which brings me to the point where this whole journey began… following a zebra called Debra…

PART TWO
A Zebra Called Debra

‘Both bold and bright,
Like black and white,
They named the zebra
DEBRA!’

As I said, the whimsical and poetic is where this all began - and where Multicolour Maths came from. In 2019, I wrote a story about a giraffe named Martha. Martha the Giraffe-a needed a friend. That friend came in the form of a zebra called Debra.

A few years later, in 2021, I started transforming into Debra on stage in a show I wrote called Birthmarked - an autobiographical musical in which I shared my experience of growing up in, and being excommunicated from, my family’s religion: the Jehovah’s Witnesses. As a theatrical choice, and to set the scene, I paralleled my story with that of the prophet Jonah in the Bible. My band and I were seen being thrown into the ocean and swallowed by a whale called Gayle (notice the rhyming theme developing here...).

Inside Gayle the Whale’s belly, I drew further parallels between my sexuality and a prominent birthmark I have on my forehead - both things that could be perceived as “imperfections.” I then used an illustration of a zebra, saying:

“If a zebra had no stripes, you wouldn’t see it and say, ‘Oh look! A zebra!’
You would see it and say, ‘Oh look! A white horse!’
Our markings make us who we are; they are part of our identity.”

I then painted my face and body and became a creature covered with bold markings - markings that are a beautiful signature of identification. That is why, in short, I became a zebra called Debra.

This adoption of a persona - one that completely transformed my physical appearance and stature - threw me into the world of queer performance and drag. I quickly realised that Debra unlocked a new, unrestrained freedom in my creativity. I designed costumes for her, wrote music in a new style, and imagined her thoughts and feelings. I even began writing in my journal to her, and from her to me. It was a creatively liberating and exciting time for me as an artist.

After a year or so of embodying Debra the Zebra, I started noticing drastic changes in my sleep. For about a year and a half I spent nights laying awake - sometimes not sleeping at all. I regularly woke at two or three in the morning and struggled to fall back asleep. When I did manage to sleep, it was very lightly - and this is when my dreams became extremely vivid.

As a child, I suffered from regular night terrors. On one occasion, I had to be pulled back inside by my dad and older brother after climbing up to the window needing air. I’ve always had vivid dreams, but they really intensified during the period of performing as Debra. I began making note of my dreams- writing and drawing scenes and strange patterns. Sometimes I’d wake up crying or laughing, and feel a strange sense of emotional relief.

On one occasion, before a gig I had planned with my band (unintentional rhyme there), I woke up feeling startled. My heart was racing, beating heavily in my chest. I thought I was having a panic attack. As I came to, I said to myself something along the lines of, “You’re not anxious - you’re excited.” I felt as if I knew the backstory of Debra the Zebra - her journey from her world to ours, and how she would eventually collide with me inside the belly of Gayle the Whale. I picked up my notebook and turned on the light, but there was no electricity. (I was living in a house share with three friends at the time, and none of us had remembered to top up the electric… again.) So, in true Jane Austen style, I lit a candle and started writing:

‘Somewhere not too far from here,
On a level plane of land
Where the sky is wide and clear,
Where the earth is dirt and sand
There live a thousand creatures -
Some humble, others grand,
And if you look just over there
A herd of zebra stand.’

The rhythm and rhyme flowed with little effort, and the whole world and story began falling into place. The laws and social structure of Debra’s community started making sense on the page. I kept writing until morning, then headed off to meet my band at the rehearsal studio. To their surprise, I told them we’d be improvising a whole new show (rather than rehearsing the old one). They laughed - and I’ll forever be grateful to them for their support in moments like that. The following night, in the back garden of a pub, we performed the tale of Debra the Zebra. 

Improvising in front of an audience has always been incredibly fruitful for me. I’ve had many ideas, lyrics, melodies, stories, and characters come into my mind - and out of my mouth - in the joy of the moment, especially when in front of people who are holding on to what I’m about to do or say next. It’s as though the ideas are pulled out of me by some kind of magnetism of an audience’s attention. That same feeling began when my nieces were born. Suddenly, I had an audience to write little stories for - and the stories just kept, and keep, coming. Telling Debra’s story that evening stands out as a truly poignant moment for me. I felt I’d glimpsed another world. And from then on, I just told myself to keep following the zebra. 

I continued performing as Debra, but in 2023, I felt a real dip in enthusiasm for the arts - something I hadn’t experienced before. I felt hopeless and a little exhausted. A part of me was unfulfilled. When I was younger, I’d wanted to be a nurse - to work with children in some kind of healthcare role, specifically in mental health. I studied an access-to-nursing course but failed to secure a university place because, ironically, I failed the maths test.

The feeling of hopelessness and pessimism (I even started jokingly telling my friends, “I’m a nihilist now”) came from a sense that I wasn’t doing “important work” - important things for society. That I was “just an artist.” And although I knew there was power in telling my story on stage - turning into a tap-dancing zebra - I couldn’t shake the spiralling thoughts.

At the same time, Debra’s story was still unfolding. I followed her up a mountain where she launched herself into the air and plummeted to the ground. Then two great wings spread out from her back and then

‘Debra the Zebra,
with her heart fully loaded,
flew straight through the stratosphere...
and then she exploded.’

I had reached the point in Debra’s story that brought her from her universe into mine - splitting the sky in two in the process. (I promise this “essay” will get more focused soon - but the story of Debra the Zebra is relevant to the maths!)

So…I was spiralling into nihilism, and my zebra was exploding through space. That unexpected and very cinematic event became a catalyst for other thoughts and ideas to come.

While researching the work of the philosopher Nietzsche (not a lot, to be honest, but enough to feel at a loss for purpose), I began to feel a growing awareness that at the heart of the universe - at the heart of everything - was a language I didn’t understand, and felt I never could. That language was also the only plausible explanation for Debra’s journey from one universe to another.

That language was, unfortunately, maths.

For a while, I found it quite comical that my alter ego’s story was entwined with my worst enemy. But it highlighted something I hadn’t given enough attention to: a deep urge, a drive, to understand things in ways I didn’t feel I was able to.

I bought a copy of Stephen Hawking’s book A Brief History of Time, and despite my best efforts, I just couldn’t process what on earth he was on about. I felt, as I had felt in school,  unintelligent in the way scientists and mathematicians are. I was, after all, “just an artist.”

But that urge to understand didn’t go away. Eventually, I gave in and bought myself a maths textbook and booked a flight to India with the intention of taking myself on an adventure and learning maths whenever I had a moment to sit in the shade.

That trip to India turned out to be quite a significant one - with my watercolour set and an injured foot, I stumbled into the world of Multicolour Maths. (You can find a small documentary about that trip on YouTube called Multicolour Maths on Munroe Island. I’ll also be writing an explanation and analysis of how I constructed the method soon.)

Within two months, I’d gone from fearing maths to absolutely loving it - all through the process of painting patterns. From that time on, I’ve felt like I’ve been on a non-stop rollercoaster: writing two books, presenting at the British Society for Research into Learning Mathematics, creating an online course, designing toys, being featured on BBC News, and now - with Multicolour Maths a part of the National Numeracy campaign - seeing it help people of all ages engage with maths in a more accessible way.

Although all of this is extremely exciting - and a little surreal - it also makes me nervous. At times, I panic that I’ve stepped into a field I have no experience in (i.e. maths education), and I worry that I might be making things worse.

But I keep reminding myself: if it helped me, it must, surely, be able to help others.

Something else that’s spurred me on was a comment from a UK teacher, the head of maths at a primary school. In response to the survey statement “Alternative methods for learning maths are beneficial,” he marked: “disagree.” Just one comment. One teacher. But I felt so driven to prove otherwise - and to continue developing something that I truly believe could unlock doors for many students.

On a more encouraging note, a few days ago - on the first day of this trek - I was contacted by an organisation called Classroom in the Clouds, which supports schools and teachers in rural Nepal. They told me how exciting it was to discover a method that makes maths engaging and accessible without the need for any fancy equipment. That made me realise something wonderful: I can travel with just a backpack carrying paper and paints - or even just a pencil case filled with ten crayons - and still teach this method. So now, as I trek through this mountain range, my bonkers idea is out there in the world... and I’m just trying to keep up.

The response from teachers, students, and parents has been so beautiful and encouraging. It’s made me pause and reflect on this thing I’ve created. And one of the main things I’ve realised - profoundly - is the importance, and educational power, of art.

I no longer feel that this “thing I do” is just a “thing” I “do.”

This “thing” is something we all do, until we’re made to feel we “can’t” or we “shouldn’t.”

PART THREE
PAINTING

“And so she learnt to whisper it and squashed it like a berry,
Until one day she stepped upon a bright and bursting cherry.
She dipped her tail in the juice and whipped and whipped her skin
And soon she felt as beautiful As she had felt within…”

Although performing has been a huge part of my expression, especially in the last few years, it was painting that really reached in and grabbed my heart when I was a teenager. I found an old set of oil paints in my dad’s garage when I was seventeen, and I quickly became obsessed, addicted almost, to the process of painting. Painting portraits especially.

Seeing a person emerge from a blank canvas, sometimes managing to capture an emotion, had a profound impact on me. I noticed I was becoming more observant of people around me, and I realised that learning to paint was also learning to see, to really look at what I was looking at. To notice light, and colour, and texture and form, it is all part of learning how to apply the paint to the canvas and create an image. 

The process of colour mixing was (and still is) mesmerising for me, almost more interesting than the “finished” painting. Sometimes I would notice that I had been painting for hours and not once really concentrating or consciously aware of how I was mixing the colours, yet finding subtle shades and tones, all subconsciously. Colour mixing became a language I was fluent in, and I didn’t have to think when I spoke it, much like a mother tongue.

Painting is a meditative process, and I know that I spent many hours from my teens through to my twenties in a floaty, subconscious meditative state when painting all the pictures I created. I “learnt” and realised a lot of things, many of which I probably didn’t even realise at a conscious level. In recent years I have dipped in and out of a meditation practice, something similar to kriya and Vipassana meditations, but I haven’t really followed a specific style or technique. I can see strong similarities between the mental state I experience when meditating and when I am truly, deeply in a flow state when painting. 

It is no surprise that I had many shifts in my belief, arising doubts and questions about teachings of the Jehovah’s Witnesses and my own faith whilst painting. It is a powerful process. Mark making in all its forms is an ancient human trait. Carving, writing, drawing, making patterns in the sand, all have a purpose. I’m going to use painting, specifically, to explain why I think it might be helpful when learning maths  -  because for me it has formed positive, deep emotional connections to the expression of it. Painting has served as a path to loving it. 

Imagine picking up a paintbrush. A slender piece of wood, smooth between the pads of your fingers and thumb. At one end are the bristles - the brush itself. Before the use of plastic, these bristles were made with animal hair: horse, hog, squirrel, and many more.

At the moment, here in Nepal, I’ve started using brushes made for a specific type of traditional painting called Thangka painting - a highly detailed style that focuses on balance in composition. It is as much a meditative process as it is an art form. Its repetitive structure and intricacy bring about a deep, focused state of mind.

The brushes used for this style of painting are made with squirrel hair. The hairs are both soft and firm at once, and they come together to create an incredibly fine point. Of course, different art forms require different brushes, and different artists have different styles - but for the sake of this explanation, imagine a squirrel hair brush. (I’m aware there are animal rights issues involved here… but hopefully you can still imagine how soft squirrel hair is!) The hairs are tightly bound at the end of the brush. Making a brush like this is an art form in itself!

When I teach people to paint maths, I start by asking them to hold the brush and say: “I love you, paintbrush!” For young children, this communicates that these tools are special, precious - and that we need to look after them. I do the same with crayons and paints. I still have brushes from when I first started painting fifteen years ago. They’ve become a little family to me - just as a cook might feel a connection to their favourite wooden spoon, or a carpenter to their favourite chisel.

So, we’re holding the squirrel hair brush. We’ve established awareness and care for it. Good. Great.

Now we dip it into some clean water. The hairs are wet and smooth. Now imagine brushing the bristles across the back of your hand to paint an invisible line. The very tip of the brush bends slightly as it slides smoothly over your skin. You can feel a gentle pressure, like a spring being pressed and released, as the hairs lift away from your hand. It should feel quite nice. Like stroking an animal.

When I ask people to do this, I encourage them to focus on the sensation: the brush on the hand, and the pressure they feel in the pads of their thumb and fingers. The slight bounce. It’s so subtle and almost minute, but it’s very much there, and very much feelable.

This physical sensation, often overlooked, is so beautiful, and it changes depending on the tool: the brush, the pen, the crayon, the way you're painting. I’m beginning to think it plays an important role in the process of connecting to learning, of taking in information, and emotionally connecting to that information. To the experience of taking in that information. To the speed and intention behind the expression of that information.

When I’ve taught teenagers it’s amazing to notice how they slow down when painting the patterns. Using the same brush for the whole image means they must clean the bristles between each new colour. Then there's the awareness of how much water to add to the paint, depending on how dark or thick they want it to be. There’s no rushing through the mark-making. It’s all considered, felt, and experienced.

The author Hermann Hesse once said that he “wrote” the majority of The Glass Bead Game while gardening - while his ‘hands were busy’. I find that very interesting. It is an example of how when we use our bodies - especially our hands - to physically do something, our brain enters a slightly different state (or at least engages more areas). Maybe this brings about a kind of flow state that allows us to take in, process, and express information in ways we might not have done had we rushed through it with a slick fast-writing frictionless pen. 

I’m not saying that form of writing is not useful - in fact that's exactly how I’m writing this right now! But when it comes to learning, especially the kind of learning involved with the language of maths, maybe there is value in using media that requires not just mental focus, but physical attention as well. I think this relates to kinaesthetic learning - the physical touch, pressure and movement connected to learning.

I don’t know much about the ancient art of Japanese or Chinese calligraphy, but I imagine there’s an emotional connection involved in that too. The process, the symbols, in the movement of the brush and the flow of the ink. Whatever the medium - paint on paintbrush, crayons, chalk - I believe there’s a direct physical feeling involved, something different from using a tool a child might perceive as just a tool for writing. The importance is the awareness of the intention, the care that is taken when creating something, not simply writing down numbers.

Before Multicolour Maths, my preferred medium was oil paint. When I first started painting, it was with old oil paints I’d found in my dad’s garage. I loved their buttery texture - and because I was determined to create pictures like the old Renaissance masters like Leonardo da Vinci or Lawrence Alma Tadema, oil paint was their medium, so I chose it as mine.

Oil paints mix beautifully and dry very slowly, allowing them to blend in subtle and versatile ways depending on how much oil or turpentine is used. They are much easier to control than watercolours - they stay where you put them (to an extent). For photorealistic painting, that control is very very handy indeed.

The process of painting portraits in oil has been very special to me. I once painted a portrait of an Indian man named Pratap Mina - a process that involved countless steps, decisions, alterations and considerations. Combined with the physical movement of my hands, it became an emotional experience. I felt deeply connected to both the image and the materials. (I would eventually use that portrait as an illustration of the difference between faith in the prophet Jesus and faith in Jehovah God while I was being judged by the church elders - but that’s a whole other story for another time.)

I love oil paints. I understand them. I’m comfortable with them. I never thought I’d use another medium with the same ‘affection’. But maths, for me, is in watercolour. For now at least.

Maybe that’s because I discovered this method while travelling, and my little watercolour set was what I had at hand. So from the very beginning that’s what I’ve used to paint maths. To learn maths. To re-meet maths. 

With watercolours, I am fascinated with seeing the pigment touch and seep into the paper. This is another reason I think painting maths is powerful. It’s beautiful to witness it happening, knowing it means something, holds information, and can be read. It reminds me of Egyptian hieroglyphs - incredibly detailed and specific images carved and painted on the walls of temples, not just for decoration, but for holding very important information. 

Although I am using painting as my primary example of how mark-making impacts learning, other materials such as crayons, coloured pencils, chalks, etc. are just as powerful in their own way. It’s the pattern-making that carries the mathematical meaning. As long as the pattern is made, the medium doesn’t matter - though I think manual application of colour is more effective than using digital means where a stylus is touching a screen. I’ve spent a considerable amount of time using digital tools to design my books, but it’s been the physical, hands-on painting with real-world materials that has been the most effective, and enjoyable for me. 

I’m also aware that some individuals may face physical or psychological challenges when using drawing and painting materials - such as individuals with dyspraxia. For this reason, I’ve begun developing physical representations of the coloured shapes to explore sculpture-building.

One striking example of physical interaction with Multicolour Maths came when I was exploring the use of small sculptures with a four-year-old girl. She didn’t yet have a strong grasp of numbers or their value, but she was able to build a 3D sculpture that mirrored the pattern in one of my illustrations: 

A man in a boat, wearing a blue shirt and a green pointy hat. Above him hangs an orange and yellow sun. 

In Multiclour Maths, read from bottom to top, this translates to:

8 × 7 = 56

It was brilliant to see her translate the image from 2D to a 3D sculpture. I then asked if she could turn the man upside down. Amazingly, she placed another green triangle on top of the “sun,” with the tip pointing in the opposite direction - and then placed a blue circle above that.

Even though she didn’t know that the colours represented numbers, she had, in effect, inverted a calculation. If she were to learn the numerical meaning of those colours and shapes, she might one day realise she already knew facts like:

8 × 7 = 56
56 ÷ 7 = 8

This sculptural approach gave me a whole new perspective and understanding. To build a calculation and see it grow in multiple directions - outside and beyond a flat 2D surface - is incredibly exciting. I believe it could help students understand maths with an expanded sense of dimensionality.

PART FOUR
COLOURS

When painting maths, I consciously avoid mixing colours. I’ve already selected the hues and shades I love. I’ve wandered through London to find the perfect pink (opera pink), split open watercolour pencils to extract a beautiful blue and a vibrant green, and squeezed the perfect purple into trays to dry on the radiator. I do everything I can to stop them from mixing with one another.

Yes, I’m slightly obsessed. But it’s all part of the art. And the reason? Because these colours are my numbers.

My sky blue is eight. Not eight point four. Not seven point six. Just eight. I want it to stay that way. Okay, maybe I’m being a bit dramatic - but the point is, the colours are important. The distinctions between them matter. They need to be instantly recognisable and consistent.

There are ten distinct colours, as far as I can tell, and I want to use them clearly.

White. Black. Brown. Pink. Red. Orange. Yellow. Green. Blue. Purple.

These ten distinct colours are a key aspect of why the method seems to work quite easily. Most people I’ve spoken to seem to agree that these are the “main” colours. They’re distinct, familiar, and accessible. No ‘teal’, no ‘magenta’ - just solid, bold, recognisable colours. Realising this was incredibly exciting, and I’ve stuck to those ten ever since I counted them.

Quite a few people have asked how I chose the colour-number arrangement. There isn’t a complicated system behind it to be honest. Black felt solid - like a single black dot. Two emerged from that dot and became brown, and pink felt like a soft beginning to the colour spectrum that would travel up through to purple. Zero, for me, felt like white, like an empty space or a void. That choice, I later realised, made the method easy to use on white paper, which is a common surface for drawing. (It wouldn’t have worked as easily if the number one were white - as an electrician pointed out to me in a very directly worded email.)

I did experiment briefly with using coloured bars to represent the size of numbers - before I’d even heard of Cuisenaire rods (another maths education method that uses coloured objects to help students understand fractions). I quickly realised that representing numbers as bars - though useful for showing quantity, fractions or ratios - placed big constraints on creativity and limited the possibilities to spot the patterns that arise in numbers and multiplications.

I’m aware that not everyone sees colour in the same way. I want to explore how the Multicolour Maths code could be adapted for people with colour vision deficiency. For example, by adjusting the red and green hues to improve accessibility for those with deuteranopia (an inability to see green and red). And for those with synaesthesia - or just a personal colour-number association that differs from mine - I encourage them to rearrange the code to fit their preference. I don’t want to say, “You must stick to these colours.” I don’t want to restrict anyone from seeing the patterns that the method can open up for them.

There’s also a strong emotional element to using colour as a language that I think may help create more of an impact when learning. Most people have a favourite colour. Our emotions are connected to colours. There are probably whole areas of psychology devoted to this type of thing. I don’t know much about it, but I know that I feel different things when I see different colours. My favourite colour is blue. Light sky blue. I feel good when I see it. A  dusty paple purple is beautiful too. Yellow is very uplifting. Blue and yellow together is very fun. Yellow and pink is brilliant, which means I now love the numbers 36 and 63, and I get excited and happy whenever they appear.

36 is a popular one because she (in a way the numbers now feel like they have genders  -  not that I am imposing gender onto them, I’m just stating thoughts I have noticed) is a multiple of 3, 12, 4, 9, 6, 2 and 18. 36 is also 6 squared. I love 36. It’s a bright, popping, fun and sweet number. I feel emotionally connected to it. I know its relationships, its family tree, something I didn’t have any connection to before this.

18, black around blue, is cool. Very cool.

I like 18.

72, green around brown, is sophisticated.

56, orange around yellow is bright and hopeful.

All of these numbers, these colour combinations, bring about emotions, stories and energies, along with the information and relationships they have with other numbers. It is making me smile as I write this, just going through in my mind’s eye all the numbers and their presences, their personalities, and my different feelings toward each one. I suppose this highlights to me how this experience, this artform, has established in me not only a love of maths, but a connection and friendship with numbers themselves.

I recently read about the Indian mathematician Srinivasa Ramanujan who said he was friends with numbers. I am in no way likening myself to Ramanujan, just to make that very clear, but I think I may understand an element of his affection for numbers. It is also very interesting to think about how Ramanujan came across his theories - many of which are still being studied and applied today. His mathematics described the physics of black holes almost 100 years before black holes were even discovered. Ramanujan claimed that he received his mathematical knowledge from a goddess, that she would write them on his tongue. Professors at Cambridge had a hard time accepting this claim, and he sadly died at the age of 32 before he could provide any other explanation - maybe because there was no other explanation. Ramanujan no doubt disrupted the way in which the other professors perceived maths, and beautifully; at the heart of it was his love and friendship with numbers.

So, if colours can help instil a love of numbers, I think that may be helpful, at least while introducing maths to young minds. Or even mature minds. 

A note on that point - I believe, because I have experienced it as an adult - that this pattern-based way of perceiving maths could help adults too. It may appear very innocent and childlike, but these patterns can range from looking like flowers in a child’s colouring book, to intricate tapestries, sophisticated tile designs, and decorations from an ancient time. I hope to find more ways to make it attractive and useful for people of all ages. I no longer see maths as something we only learn at school. It is a timeless poetry that is waiting to be appreciated at any stage of life.

PART FIVE
CIRCLES

A few days ago, just after I had arrived in Khumjung village, a small girl about two or three years old sat watching me write. She then pointed to a cow and made some expressive noises and  started drawing a circle in the air with her finger. I don’t know what she meant by "cow" and "circle," but it made me smile.

It can be a mesmerising thing to watch someone draw or paint a circle. I’ve loved watching people of all ages really take their time to produce a beautiful circle - slowly moving the brush to complete the loop, filling it in, and gently adjusting and balancing the edges until they’re satisfied. It is beautiful to watch, and beautiful to do.

While teaching a class of teenagers in Namche Bazaar, the whole class applauded as one of their classmates painted a beautiful circle on a large piece of paper. It was a really lovely moment - a fascinating example of our appreciation for witnessing something come into form - in this case a neat and balanced circle.

I’ve been painting circles in my art for a long time, often using them as halos behind someone’s portrait. Circles can give us a focal point - maybe they attract our attention in a subtle but profound way. Maybe this is because we connect with each other through circles, by looking into each other’s eyes. Looking into the eyes of a loved one is a significant thing in life. Sometimes, we purposely avoid looking at eyes. We either trust or distrust them. A lot of information is contained within the circles in our faces.

I guess my point is: circles are powerful shapes, and in a way, possibly the most elementary shape. The little girl drawing a circle in the air with her finger would probably struggle to draw a rhombus or a square. But maybe circles are things we learn to understand very early, because they are so embedded in our visual world and experience. Maybe. I don’t know. But I do know that it seemed most obvious to me that numbers would be circles in my method.

I will cover how the method came together in another essay, but at one point, after painting a very intricate multiplication table with triangles, I decided to represent numbers as circles, and circles within circles. Like the pupil in an iris. And it worked. Very well. Not only are they a very meditative shape to draw, but they allow for the pattern to be read in any direction - something I didn’t realise until I saw one of my own pictures upside down.

The balloon and triangle - both shapes inspired by Indian culture, like the bindis and temple roofs - are also the only basic shapes I can think of that are clearly directional. They have clearly defined opposite ends. Their functions - addition for the balloon and multiplication for the triangle - are also reversible: addition becoming subtraction, and multiplication becoming division. Again, this is something I didn’t realise until I saw one of my pictures upside down. I understood that subtraction is the opposite of addition, but my understanding of maths was so limited that I didn’t know that division is the reverse of multiplication.

When I first saw my painting which read 4 × 7 = 28 upside down, I had to Google whether the opposite was correct.

Upside down it read: 28 ÷ 7 = 4

It was quite a revelation to me to realise that the formula applied to every multiplication.

Although seemingly simple and basic, this is an example of how seeing something visually can aid understanding, and something I believe could help others. 

The contrast between the feeling of the shapes is quite significant too. The teardrop and triangle appear active, whereas the circle is calm, static, almost floating peacefully. I think this helps with reducing anxiety, especially when actually being drawn or painted.

Another aspect that I think may help with reducing anxiety is the fact that there is instant gratification. Even just painting a single circle, a single digit number, is so rewarding, as the example with the teenagers applauding their classmate demonstrates. To express maths and feel rewarded at any step is very special, and maybe helps the information sink in deeper as opposed to if it were scribbled in pen or pencil. (No offence to pencils. I love pencils.)

Anxiety is also avoided by transforming mistakes into moments for creative expression. When I realised that I was, after all, creating artwork when doing the maths, I felt such a sense of relief and excitement in being able to not only continue a calculation despite a mistake, but I was able to expand into more possibilities because of the mistake. To know that no calculation, no piece of artwork, had to be discarded or disregarded due to a mistake completely diverts away from any feeling of unintelligence. I think this might be important for children, and especially for adults who are trying to re-learn something they may already be traumatised by and have low self-confidence in.

I am not a trained pianist or guitarist and I constantly make “mistakes”, but these “wrong notes” have so often led to new melodies and whole new songs. And in terms of painting - a portrait does not come out of the paintbrush and onto the canvas in one perfect fluent flow: it evolves through hundreds, thousands, even millions of “mistakes” until the artist is content and ready to step away from the image. When learning a language it is essential to feel safe enough to make mistakes too. When I was learning to speak Mandarin, it was the comedy of mistakes that helped me enjoy the process, and eventually I found a level of fluency and understanding. I think the way in which mistakes in maths are visually presented can be viewed and treated in the same way. Maybe moving away from the need to find one right answer could help too...

PART SIX
MATHS WITHOUT ANSWERS
The Landscape of Mathematics

What does maths become when it is not treated like a machine that we have to learn to use to get “outputs”, “results” or “products”? My impression of maths from when I was at school was that it was a subject, a part of the academic world, a function of the brain that was filled with problems. You had to use all the parts of the machine to “solve” these “problems”, and if you didn’t get the correct answer, then you were “wrong”. You tried again, and again, and again until you either reached the correct answer or you didn’t, and that was the end of it.

Maths was a landscape filled with jagged rock faces, sharp corners, and danger everywhere. It was rock, solid, unforgiving and heavy. The land of maths was somewhere I didn’t want to be. I realise of course that problem solving is a very important element of maths - it is an incredibly powerful tool for finding solutions and inventing things. But in terms of introducing people to the land of mathematics, I wonder how different their experience and relationship to it could be if the focus was moved from solving problems to exploring it visually and discovering its patterns. How different could that landscape look?

By focusing too strongly on maths as a “machine” that solves problems, we miss the importance and beauty of the interconnectedness of numbers. Do we miss the chance to see, appreciate and understand the invisible web, the mushroom-like network that lies beneath it all? The landscape could be more like a forest of trees with interconnected roots, not single separate trees in concrete boxes. From a different perspective, maths can become as forest of numbers. An organism. Connected. Alive. Awe-inspiring…

Even a mountain range can transform. When you look at one single mountain, a gigantic monstrous rock erupting from the earth, it seems inconceivable that anyone could climb them. They look terrifying. But as I am learning from the people who live on them, these mountain ranges are great ridges, like the spines of giants laying over the land - from a different perspective these mountains might look a lot like the ridges of our fingerprint. From above, the mountains are not monsters, they are patterns. The particular ridge I’m looking at right now is called Kangtega, which in the Sherpa language means “Snow Saddle” - a story and character has been attached to it, the idea of a horse and rider, a story that no doubt plays a significant part in building an image and an understanding of the landscape,one that helps the people who live here, live here. These visual stories help with navigation in a place that newcomers like me would have a very hard time travelling through without the knowledge of the local people.

And if we were to watch these mountain ridges over millions of years, with a different perspective of time, we would see them moving like ripples across a pond. Even these giants of rock are not solid, they are alive and fluid and changing.

As I have been writing this on my crumpled piece of tracing paper, the mountain, the gigantic horse Kangtega has disappeared again behind the clouds. A beautiful way to consider for a moment what the landscape of maths could look like if we could see numbers from above and gain a whole new understanding of what’s going on.

Thanks to the colours, I feel like I am not only able to see maths as a beautiful landscape, but I am able to see it from many perspectives, above, through, below and around. This perspective could have been transformative to my journey through school when I was younger. How different my time in school could have been if I had the tools to fall in love with maths as a child.

PART SEVEN
INSECTS AND ELEPHANTS

This next section is taken directly from my journal…

29th April 2025

As I write this I’m looking at a beautiful blue beetle that was just crawling along my notebook. Its beautiful wood-looking shell opening up like a car bonnet and two clear wings extending out at 45° to each other and moving so fast to propel the body forward, creating a buzz like some kind of engine. I can hear him humming across the floor now. It is 6am and he has arrived and reminded me to write about one of the things I’ve been thinking. (A monkey has also arrived and is throwing himself through the trees. OMG it just landed on the roof and I thought it might be a tiger because of the way I saw its tail but it’s ok it is a monkey... I’m safe.)

The maths has opened my eyes to symmetry in a way that seems to be endless and unfurling. Flowers, leaves, fruit, our bodies, and most stunningly I think, insects. I see them almost like alien robots now. Truly truly fantastical feats of engineering. (Wow a whole family of monkeys is coming past me through the forest!)

And not just because of their shining shells, they are also beautifully soft and deft and gentle, and also seemingly indestructible at times. The spiders that are so quick and flitty and jump with their hydraulic-looking legs and shining blue and black patterns which are also symmetrical. And of course the butterfly’s wings that are such works of art. And the tiniest tiniest red spider that was crawling along the tip of my pen the other day - also completely symmetrical. And the symmetry doesn’t stop there. It continues in frogs, in birds, in dogs, in us, in tigers, in elephants. From insects to elephants and far, far beyond, the symmetry is there.

My thought was: if this symmetry is so apparent in the world around us, why don’t we study it more? Not only does it give us a deeper appreciation of how connected and poetic the universe is, but it provides a foundation for understanding maths.

For example, my brain has not only understood that 4 × 7 = 28,  28 ÷ 7 = 4  or even just 2 × 2 = 4, 4 ÷ 2 = 2, but I have been able to really comprehend what that means in the world around me. As in that symmetry. And not just to write 4 × 7 = 28, 28 ÷ 7 = 4 in the written left to right form, but to see it from all directions. It’s a mandala, growing out and returning to the centre. From the centre to the centre seeing the whole.

4 × 7 = 28 ÷ 7 = 4 × 7 = 28 ÷ 7 = 4 × 7 = 28 ÷ 7 = 4 × 7 = 28 ÷ 7 = 4

Even just being able to write that sentence with a pen was so nice to do just then. (It made me realise that I should try and create a black and white version that really can be used with just a pen. That would be very handy. All I would need is nine symbols that are symmetrical (and reversible) to themselves that can be read in any direction?) Anyway...

There is also an aspect of cause and effect. ‘If this, then this’. As in it doesn’t just stop with “28” being the ‘answer’. It continues and reverses, expands and changes and then leads to yet more change and also back to the beginning again.

More development, more growth or reduction. One part goes on to become a leaf, the other forms a stalk to grow bigger. There is no end. No answer. There may well at some point be something in a calculation that we see as a “fruit”, the visual bit we want to pick out, peel and eat for ourselves. The big bright yellow thing we were hoping to see from the banana tree, but that doesn’t mean the rest of the tree is useless, that the rest of the calculation does not hold just as much value as the “result” or the “output”, as I heard teachers say. “Input and output”. Such a dead way of looking at it all. To me at least.

What is the ‘input’ of a piece of music? What is the ‘output’ of a piece of music?

“The Lark Ascending”  by Ralph Vaughan Williams –  what is the input and what is the output? It is all one organism.

Our focus and obsession with finding the answer seems to be distracting us from the whole beautiful music, the orchestra. It is like taking a child to hear an orchestra and saying “only concentrate on the solo part that the violin plays. Don’t worry about the other one hundred musicians that are supporting them.’ It’s crazy... What if we were introduced to maths and got to know it as something it has always been and will always be? A language filled with beautiful patterns. Surely our brains are wired to recognise patterns. I don’t know for 100% sure, so I can’t say “surely”... but surely!

Surely our brains are wired to see patterns, and yes Brook, you’re pretty sure they are! So why not utilise that natural tendency and ability when introducing maths to children? It could help establish not only a deeper, more fluid understanding, but a love for the language much earlier, and to many more kinds of minds, more minds who will be able to manipulate that language in so many uniquely individual ways. A pack of coloured pencils in the hand of one child will not result in the same images as the same pack of coloured pencils in the hand of another. That’s because art and mark making are endlessly omnidirectional and the possibilities of what they create are unbound by the left to right, top to bottom, end at the “answer” and put your pen down when you’re “finished”. No!

Don’t put your pen down! In fact keep colouring and painting and creating art until your hands are tired and you are so hungry and exhausted that all you can do is collapse at the foot of a great mural and lay looking up at it and stare in awe at the beautiful language you have expressed and felt and been moved by and love. Don’t put your pen down. Pick it up and translate that mural into the written form, which also one day might change. One day it will change. Like why the hell are 9 and 6 the same things upside down? That is so unhelpful for some people!

And x and + are just 45° angle different?! Haha! Back to the point...

Many more minds might be able to love the language of maths, and be able to find their own unique relationship with it. It doesn’t have to only be something used to find answers to one single question. And I am not saying it shouldn’t be a language used to find answers, I’m just saying it shouldn’t only be a language used to find answers, to solve problems. The spoken language is not only used to solve problems, or answer questions. Of course that is a powerful use of it, but the spoken language is also used to tell stories, to sing and to express emotions!

The language of maths is not just a hammer - a tool to drive nails. It is also a piano. Ah! Actually yes, it’s a beautiful piano filled with hammers. The hammers of a piano are soft and articulate and each one moves beautifully to create music. A single note can be so powerful. A whole arrangement of them moves the heart. Maths can be a hammer and a piano. The operations are like piano hammers - you press a key on the piano and the hammer strikes or softly touches the strings and the music begins. The piano sings.

Still the subject of “answers” hangs in my head. How should or could we approach them and our relationship to them, the search and need for them, in a way that is healthy and less grabby? Needing. Is there a way to frame the answer, or the searching for answers in maths at least, as a thing of like “Oh! of course!” or more arriving? Hmmm, no because that still seems to convey the idea that you have arrived at the end. There is no end.

I'm going to listen to The Lark Ascending and see what I feel. Maybe I'll sit and close my eyes...

…

I've been listening to it on repeat. I'm on my 3rd go.

The first time I just listened to it. I was crying within the first few minutes. It is such an incredibly moving piece of music.

A few music words that I thought  -  flow, journey, support, theme, variation, return, harmony. Many of those are of course terms used in music, but I think they can really apply to maths.

One of the things that really moved me was the fact I am listening to the rest of the orchestra supporting the violin. I hadn't really focused so much attention on the rest of the orchestra. Of course I had heard it before, but this piece of music has a clearly defined lead line or part, the violin. The lark, flying over landscapes, twisting and turning, ascending and falling, gliding and slicing through the sky.

It also made me think about balance. The orchestra is providing a landscape, a base and foundation and atmosphere in which the violin exists and soars above and through and with, and at one point, around four minutes in, it drops swiftly away, and the orchestra swells and bursts and waves into movement and a large cloud, a fullness comes into the space and the violin disappears. The lark is behind the clouds, dissolved into the whole, and then returns. The lark has a flight that is in harmony with the orchestra, the atmosphere, and that journey is changing and fluid. But it makes me think: it is only one journey of a myriad of possible paths, but all of which, well many of which, would most likely be in harmony with the atmosphere, with the laws of physics, in terms of the real flight of a bird, in the sky, just as there are infinite possible melody lines that could be played harmoniously above the orchestra section. Which leads me to think about balance…

Realising that 2 + 2 is not only equal to four, which, yes, it is equal to four, but it is also equal to 1 + 1 + 1 + 1, and 3 + 1, and 1 + 3, and 6 – 2, and 5 – 1, and 8 ÷ 2 and so on and so on and so on and so on and so on forever, which moves away from the idea that there is only one right answer in a maths equation. Maths equations. The whole concept of the equals sign as if it shows one answer, one “output”, is misleading to the idea of balance. Of course there will be one “whole”, single answer, but even then that answer can be broken down or shared or expanded, so an answer is not always the sole result. Searching for and demanding one answer from a calculation and not considering all the other ways, or at least some of the other ways it could be balanced, is restrictive and demands so much conformity. I'm not saying that untruths should be encouraged, 2+2 is not equal to 3, with a full stop after it. But it is equal and balances with 3 + 1, and that truth could be beautifully mind-opening for a child who is coming to meet the language of math.

Thinking in terms of “teaching” children, allowing them to explore the possibilities, whilst of course explaining the value and utility of a single or simple “whole” answer  -  hmmm that word still doesn't seem right, maybe if thinking about the music, a “movement”, an expression, an expressed moment, a moment of expression. Maybe that is better. An expressed movement, a moment in mathematics.

For example, when looking at 2 + 2 = 4, we could say 4 was an expressed moment, and we could say the ‘+ 2’ is the “movement”.

When read in reverse, the 2 is also a "moment."

“The phrase at this moment is 2.”

“The phrase at this moment is 4.”

That’s three terms: Phrase, Moment and Movement.

It also helps to conceive the idea that whatever piece of information we are choosing to take as our “banana”, the fruitful piece of ‘useful’ information of a certain section of maths, is not the be all and end all of that phrase. The banana contains seeds that will go on to bear fruit. It is a singular moment in “time”. ‘At this moment it is this, but it will change and it is also part of something much much bigger. The whole universe of the language is connected to that moment. A leaf is a moment of expression of the life that is the plant, which itself is a moment of the expansion of the life energy from the soil.

The flower is a moment. The fruit is a moment. All are moments. Moments of time and expansion.

The fruit is not the end, in fact it holds the seeds to become the beginning again, and in turn indicates that the language is eternal. Forever and unending, and when it somehow maybe reaches its end, expresses its true identity as something divine.

(Not quite sure what that last sentence was trying to imply...! Just kind of came out…)

• End of journal entry •

PART EIGHT
MATHS WITHOUT ANSWERS
Compositions

We don’t tend to listen to or compose a piece of music to find an “answer”, or the answer of a piece of music. It would be strange to listen to a piece of music composed by Bach, a very mathematical composer, and ask “what note is the answer?” We don’t listen out for a single note and say “that is the result.”

Even if you did select a single note for some reason, that note would sound very different if disconnected from the rest of the composition, even if it was played in exactly the same way.

Even if we focused only on the melody line of a piece of music, we also take in the whole thing, whether we are focused on the other parts as well or not. We are moved emotionally in ways we cannot sometimes describe or put into words. In some cases music without lyrics can move us more than music with words we understand. If wordless music has the power to move us, then maths can too.

As I said earlier, I have many times been moved by painting maths in colour, partly, possibly, by the patterns and connections and understanding them as they unfurl and repeat.

In a similar way, if you were to see a single patch of colour, for example a patch of yellow, it would create a particular experience. Whereas if you were to see the same patch of yellow surrounded by greens, browns and blues, as in Van Gogh’s ‘Sunflowers’, that would create a very different experience. And those green leaves and the blue wall and the orange and brown table top are all as equally important as the bright yellow sunflowers in the centre. Together they create the whole, just as the 3 and the 5 and the 8 all have equal importance in 3 + 5 = 8.

Standing back from the painting helps us not get too obsessed with one tiny section. We take in and experience a space, an atmosphere and a feeling.

Something that is helping me keep this wider, peripheral vision approach and perspective of maths is referring to different sections not as questions or problems and answers or outputs, but as compositions consisting of phrases, movements and moments, much like in music. The whole image is a composition, like a painting arranged on a canvas. A “phrase” is a section of that composition, the joining of two or more moments. A “moment” is what could be seen as or referred to as an “answer”, or “output” or “result” in traditional maths. And a “movement” is a number in action, or a function or operation. For example, “+5”.

Just by changing the words I was using when talking or thinking about a calculation has helped me transform the landscape of maths from one of solid rock to a landscape of fluid organic elements.

I also wonder what the impact is of focusing on answers as opposed to the relationships of numbers. It feels like maybe focusing on answers all the time, the pressure that is placed after the equals sign, is like only using the type of near sighted vision required when threading a needle. How could the understanding of maths change and improve if there was also a way to use the type of vision that is used when taking in a mountain range. As I’m writing this I’m switching between both types of vision as I look down at the page and up again to the mountains in front of me. A landscape that is constantly changing as I am walking through it…

PART NINE
RHYMING

Despite struggling with maths, I was able to make things such as my “flying machine” (the one that ended up in the bin) simply with logic, imagination, symmetry, balance, experimentation and of course, many mistakes. My teachers recognised that I was capable of making things, but maths was just something I couldn’t seem to understand.

I was one mark away from failing maths at GCSE foundation level, and I only passed because I had a brilliantly engaging and kind teacher, Ms Lynch. She was funny and quick witted and had a beautiful Irish accent, so that helped. She inspired me to try, and I wanted to get better at maths because of her attitude towards it. One lunchtime I thought it would benefit me, for some unknown reason, to stand on a chair and read aloud every digit of pi which she had printed out and stuck around the ceiling of the classroom. (There was no doubt a performative element to this, not that anyone was bored enough to watch me, but I think it made Ms Lynch laugh so that was enough for me) Ms Lynch inspired me to engage with maths, and that’s what engaging with maths looked like for me.

In one lesson I remember a teaching assistant trying to help me. I was struggling, as usual, probably with my head laying on the table in despair and mental exhaustion. I remember him saying something along the lines of “Come on Brook, surely you can understand this – maths is all about patterns. You write poetry, you dance, you sing, you draw. It’s all the same. It’s all patterns.”

He really was trying to help, and now I completely understand what he was trying to help me see. The only problem was he had no way to show me. As is the case with many things, you cannot tell someone to believe or understand something, they must see and experience it for themselves. So here I am, fifteen years later with a set of watercolours and finally I see it, literally seeing the patterns he was referring to, and I am so grateful that he tried so sincerely to reveal it to me all those years ago.

I think I also now understand what he meant when he was trying to link poetry to maths. A calculation in Multicolour Maths can be read in any direction, and no matter what direction it is read, there is no end. It has no beginning. The calculations, the “phrases”, flow to and fro.

An example of 4 × 7 = 28,  28 ÷ 7 = 4, in colour, looks to me like a visual poem, a balance.

Red green brown blue brown green red

The symmetry, the ‘folding’ of the image reminds me of poetry, of a rhythm.

"CAT sat ON the MAT"

When heard audibly, it can almost represent the poetry of the colour calculation.

When the sounds are seen in colour, it even shows the folding, balancing structure of the maths. 

Being able to fold a calculation on paper and see both sides meet as though a mirror to each other also reminds me of Japanese origami - another thing I found fascinating as a child, and something I now realise is maths in physical motion and form. (I wouldn’t be able to tell you how, but I kind of feel that it must be.)

The multidirectionality of the patterns also reflects how we naturally “read” the world around us. We do not view the world from left to right, top to bottom. We have a central point of focus and our peripheral vision takes in the area around that focal point, all of which is processed by the brain. We do not simply look at the world with our eyes fixed straight ahead - we move our focus point in all kinds of directions. The way we physically look at the world is not linear, it is multidirectional. Our eyes take us on a journey depending on how we are looking at things. Being able to read a Multicolour Maths pattern feels like a journey, and each composition and style has a different “feeling” to its journey, and how it is read also impacts that feeling and journey. Some patterns are more appealing to read vertically, some horizontally and others from the centre outwards, and that is down to who is doing the reading. Directionality ‘is in the eye of the beholder’! 

It is interesting to see that people are able to read Multicolour Maths patterns without moving their eyes - keeping focused on a central point and using their peripheral vision to read in an outward direction (which now that I think of it is something I think Kriya meditation helps develop, an increased awareness and strengthening of your peripheral vision, both with the eyes open and closed).

Another interesting consideration is the fact that the patterns allow people who read their native language from right to left to read maths in the same direction. For example, an individual who learns to read Urdu or Hebrew must learn to read and write maths in the opposite direction. I wonder whether this could be helpful for people who struggle due to this fact.

This also links to the point that people who write with their left hand may struggle writing left to right and taking in information due to their hand or arm covering what they have just written. Leonardo Da Vinci was left handed and famously wrote backwards - which is sometimes called ‘mirror script’ - in order to avoid smudging the ink across the page, something that obviously helped him but I doubt students are encouraged to do today.  When I write or draw, I try to find a place where the light lands above or to the left of my pen or brush because I want to see as clearly as possible. 

A painter does not paint a picture from left to right, top to bottom like a printer. I move my brush around the whole canvas and build the image up in all different directions. It would be interesting to see whether left handed people move across the page in the opposite way of someone who is right handed, and if so, does this indicate that writing text or maths left to right involves a level of restriction for them. If someone’s hand is covering what they have just written, how does this impact their experience of writing and mark making and therefore the processing of information?

The multidirectional element of Multicolour Maths has also led me to explore how circles within circles could be used for transcribing music, and how that could influence how music is taught, understood and experienced. This is something I really want to dedicate more time to as it could maybe help people learn to read, record and write music, and it could also create a whole new way in which people could experience it, especially those with impaired hearing. Maybe.

PART TEN
=

I wonder whether the absence of an equals sign in Multicolour Maths might also be significant. It removes the separation of the “question” and the “answer”, and highlights the flow and relationships of the numbers. It allows for endless possibilities of connection from one number to the next. Any circle of colour can branch off into its possible relationships, and those relationships can branch to their relationships and so on and so on, allowing for expansive expression and calculation. 

I  discovered this possibility when I was doodling in my first maths sketchbook and I created my first ‘maths mandala’. I was extremely excited and inspired. I went out and bought a long folding sketchbook containing one long concertina of paper. I began with a single black dot - the number one. From there I let the calculation grow and expand, and I just let it flow. I switched between wanting to achieve mathematical links whilst also determining what calculation I needed to make in order to bring more of a certain colour into the composition. I was at once considering the art and the journey of the maths.

One afternoon, as I was aiming to reach the number eight because I wanted to paint a large blue circle, I had a subconscious thought about the possibility of other life existing in the universe. I am not a sci-fi fan and I’ve never really have much of an interest in outer space (I was always more interested in wild animals than aliens. More Lion King than Star Wars). But I stopped painting and looked up from my sketchbook. Quite literally out of the blue (I was painting a blue circle) I had a profound moment considering the fact there could be life beyond earth. (As I am writing this I am aware of how ‘out there’ this could come across, and I didn’t tell people for a while because I couldn’t quite work out how to let the thought settle in my mind.) It wasn’t until a few months later when I spoke to my friend who had just finished a maths degree at King’s College University in London, that he reassured me I was not thinking anything too out of the box. He explained to me about probability theory, and how mathematics supports the plausibility of other life in the universe given the sheer scale and frequency of habitable conditions. If we exist, then it is mathematically likely that other life exists too. He was amused and quite entertained that I had reached this realisation by painting my colourful patterns. And so was I. 

On another occasion, whilst painting a calculation that looked a bit like a lattice, a woven fabric of:

6 + 4 = 10, 10 - 4 = 6, 6 + 4 = 10, 10 - 4 = 6
and so on and so on…

I was deeply moved by the thought that all life forms on earth, all organic materials are built with similar elements from the same collection of atoms, and are therefore all connected. This also encouraged me in my attempt to use the Multicolour Maths code to represent chemistry - an attempt which led me to invent Colourful Chemistry and discover a kaleidoscopic lens through which to see the world’s atomic structures as colourful patterns. The catalyst for moments like this has been seeing the interconnectedness of number through a colourful language that flows in every direction.

This flow of expression, in growing, changing, evolving form, like my concertina sketchbook or the 6 + 4 = 10 lattice, could be likened to the free flowing stream of consciousness style of writing made popular by the author Virginia Woolf. I remember writing a short story when I was in primary school and at one point I had changed my mind mid-sentence. I hadn’t erased what I had previously written, but instead I found it interesting that I was able to show a change of thought in the text . The sentence was something along the lines of

“She liked, well, no, she didn’t like, but she found it interesting that…”

I was very proud of the way I had written the sentence, and the way it portrayed my thought process, but I distinctly remember my teacher telling me it wasn’t a “proper” way to write and I had to change it. It’s funny how some moments stick in your memory. As an adult I look back and think how restrictive that was. 

I think this highlights something to do with allowing flow when learning and expressing something, especially when we are young, the ability to change direction, and what that freedom can do for the mind. To consider things from more than one angle and not shut down or restrict an idea to a single line of thought just to fit an established framework. To think less linearly and more holistically, cyclically and laterally.

Equals means balance, so the space after the equals sign is not, as I have always felt, a void that says “tell me THE answer.” It is an opening of the space that says ‘what does this balance with?’

2 + 2 = 4

But 2 + 2 is also equal to 3 + 1, or 5 – 1, or 1 + 1 + 1 + 1.

Of course that may not behelpful to teach children to approach maths in that way in all instances, but to realise that there is more than one way to find balance could be incredibly freeing, and open up a whole new perspective to the equals sign. How creative could a child’s problem solving skills become if they learnt to experience maths as an artform?

PART ELEVEN
PATTERNS

My love of symmetry has also developed since painting maths and I now notice and appreciate patterns so much more. Particularly in the natural world. The patterns and symmetry of insect bodies, their wings, the structure of leaves, petals and the colouration of flowers. For instance, a few weeks ago I spotted a beautiful flower floating on Begnas lake. I later found out that it was a water hyacinth. I painted it with the intention to turn its colours into a calculation: yellow within purple, 96. 

96 ÷ 6 = 16. A satisfying repetition of 6 and therefore yellow.

Then two days ago as I was hiking up to Gokyo lake, I noticed orchid-like flowers growing on the hillside which also had a colouration of yellow within purple. Then as I reached Gokyo lake I saw lots of himalayan primroses which look like tiny daisies. Again, these had purple petals with a yellow centre. And in the lower parts of the region I have seen many purple and yellow potato plant flowers. I became very curious about this pattern of patterns. At first I thought it was a coincidence - it seemed unlikely that the flowers knew the others were purple and yellow and decided to copy each other. But I have now learnt that this specific colouration, yellow within purple, is not a coincidence. Purple is a colour that bees and pollinators are very sensitive to, and the yellow highlights where the nectar and pollen is located, like a bullseye. The combination of the two colours creates a bold contrast that helps the flower stand out against green backgrounds, and in high altitude environments, the flowers need to be as visible to pollinators as possible in order to survive. 

Learning this has been so interesting for me, and reveals how nature uses colour theory in the same way a painter does. And the close similarity of the arrangement of the colours, yellow within purple, is such a clear pattern and formula, just as I have been using in Multicolour Maths.

This has made me wonder whether painting maths and being so considerate of pattern in this artform has made me more observant in a way I wasn’t before, even though as a painter I was always looking out for things to paint. This increased appreciation for patterns has led me to an interest in botany - something I have not really paid too much attention to beyond the surface level. These few examples - insects, leaves, flowers and the human body are so much more connected for me now, which makes me wonder whether the study of symmetry, especially the symmetry found in nature, could have a significant place and role to play in forming a basis in early education - encouraging us to really observe and explore, notice and appreciate and love the variety of patterns in the world around and within us. We would then feel that we are not just studying what we observe, but studying what we ourselves are.

For myself, seeing numbers connect in multidirectional ways through colour has sparked a fascination for chemistry, albeit very basic and vague. I never quite realised that the elements on the periodic table are arranged according to the number of protons they have – beginning with hydrogen with one proton, helium with two protons etc etc. The number of electrons on the outer shell also determines where they sit on the table, and those numbers determine how they interact with each other, and the patterns and structures they form - for example the pentagons that frozen water molecules produce create infinite varieties of snowflakes. I’m talking as though I actually understand chemistry here, but I don’t really to be honest. I’m just beginning to scratch the surface through colours, as I did with maths. 

I can’t quite communicate what I think I understand or feel at this point, but seeing the interconnectedness of numbers has made me connect with the seemingly endless patterns found at all levels. The order and symmetry of numbers in atoms and the way the atoms are formed, how they create molecules which build materials, the symmetry of our bodies, the similarities of our bodies and other animals, in plants, the order and movement and balance of the planets….

I haven’t quite been able to put this thought into words yet, but whatever the thought is, I am now appreciating and feeling an understanding, which creates a sense of awe and motivates me to learn and understand in a way I haven’t felt before. And this has all started with a very simple understanding – that maths is not linear.

That linear understanding came from the written form that I had always experienced and expressed maths. It was the translation of this thing, this phenomena that is maths that impacted and shaped my understanding and relationship to it, and dulled my appreciation for how it is actually in action throughout the universe.

As I’m writing this I am aware that I might be sounding grandiose, as though I “finally understand the universe!” – I am not at all trying to convey that. I should also clarify that all of these thoughts, feelings, understandings, and perspectives have all come about and been inspired by doing basic maths. I have only experimented, painted and explored patterns using single addition, subtraction, multiplication and division. I am aware of the simplicity of the level of maths I have been engaging with.

Having said this, I am also aware that it could develop further. Traditional notation is at the end of the day a collection of signs, an alphabet created by people. People who invented a mark, a shape, a symbol on the page to represent information. So my code, my colourful “language”, can also develop and evolve in whatever way might be helpful. A teacher in Canada told me her students had learnt the method and started inventing their own shapes and codes to express different things, which shows how the method can be adapted, built upon and used in different ways.

I was given a matrix equation to solve by the friend studying at King’s College . I didn’t know (and I still don’t really know) what a matrix equation is, but I was able to arrange my colours and arrive at the correct result. My friend was impressed, more so than I was to be completely honest, but it indicates the potential for the method to be utilised in higher-level mathematics, a potential much greater than I have assumed.

And the possibilities of its use for representing patterns in numbers is greater than I have explored currently. I have been painting and drawing by hand, but it could easily be used in a digital form and coded into programmes and, dare I say it, AI. I have also wondered what it could look like if used to map out large sets of data. Different kinds of graphs could be designed that show the coloured patterns within the numbers themselves. (This is not an area I am very sure about, which may be why some of these sentences are a bit clunky, but I have vague little ideas about how the code could be used to show patterns within data, and how arranging the circular numbers could require new types of graphs or "compositions".)

Despite not quite knowing how best to put some of these thoughts into words, I feel confident that at the heart of it is something quite simple and true – that everything is related in form and structure and material, through mathematics.